dm319
The Strange Case of the Rogue HP-12c
2024-09-11
“That’s a non-trivial computation”
~Prof Kahan on the time-value of money calculation
The HP-12c is probably the most iconic financial calculator. Not being in finance myself, and in fact being terribly bad at that kind of thing, I never quite got the purpose of these special-purpose devices. My ignorance came to a halt due to an unfortunate combination of my fixed-rate mortgage period ending and Liz Truss happening, and I was driven to a sudden keen interest in the ‘time value of money’ (TVM) calculation.
My story begins when I programmed my scientific calculator to solve the TVM unknowns. As a demonstration of pocket calculator programming, the manual of the venerable HP-42s scientific gives two ways you can write your own TVM solver. While great as a programming tutorial, it was less good at TVM solving from both an accuracy and a user-interface angle. I set about improving this program, and as a result learned far more about TVM solving than I could ever have imagined. A slight change in the algorithm can easily introduce significant regressions and I quickly realised the need for a good set of tests.
Testing TVMs
Reading all I could on TVM solving, collecting example problems from here and there, and making some of my own, I constructed a battery of 13 TVM problems which tested edge-case scenarios designed to instill fear in any garden-variety TVM solver. With the help of many from the HP museum and Swiss micros forums, I set about testing as many financial calculators as I could find, learning a lot about their design in the process.
But that is another story.
What you need to know is that the HP-12c is the most iconic of all financial calculators. It is probably the longest-running continuously-produced calculator, starting life in 1981. Not their first financial device, Hewlett-Packard (HP) had refined their TVM solver to the point that the HP-12c was well placed to develop an enviable reputation as the ‘de-facto’ financial calculator. The calculator was written into high-value contracts1, with the expectation that these machines would return the exact same answer into eternity.
In order to maintain this reputation, HP have taken meticulous care in porting their code across several electronic platforms necessary to span 40+ years of production. The grail of finance machines was not to be messed with.
An Intriguing Reddit Post
Earlier this year I came across a fairly benign-looking reddit post describing some difficulty changing the decimal point to a decimal comma on a new Brazilian-bought HP-12c. Most of the replies were along the lines of ‘you’re holding it wrong’, but something caught my attention. They weren’t the only one, and not only had someone else had the same experience, I was pointed to numerous Amazon reviews describing similar woes.
To find out for myself, I VPN’d myself over to the Brazilian Amazon and started reading (with the assistance of my phone and google translate) reviews. What I saw was quite consistent - people couldn’t change the point to the comma, and the calculator also failed on something called the internal rate of return (IRR) calculation.
I was curious, were these a different version of the HP-12c? Was it a fake? It is generally accepted that the HP-12c (and to some degree the related HP-12c platinum) will return exactly the same results no matter. Why would it otherwise? It was at this point I needed help, and a very kind Brazilian redditor did the work needed to run the aforementioned TVM tests as a forensic tool. What they found was a set of results entirely different to not just the regular HP-12c, but to any other financial calculator we had tested.
This was hard to explain. The results were not unreasonable, but undid many decades of advancement in the technical progress of this ‘non-trivial’ problem. The natural inclination was to suspect a fake device, something which is rife in the world of modern Casio calculators. However, fake HP-12c’s are not that prolific in the wild, and further examination of the reviews suggested that despite official replacements from HP, the calculators continued to malfunction.
Lets have a look at a few of these TVM puzzles to get a better idea of how it is different.
A Penny for Your Thoughts
If you saved one penny every second for a year, in an account with an interest rate of 10%, how much would you have by the end of the year?
This is a ‘solve-for-future-value’ problem, and it has a couple of technical challenges.
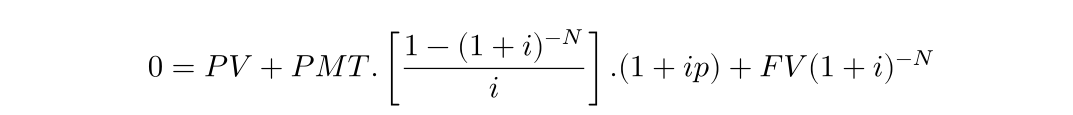
Above is the TVM equation itself in all its glory. You’ll notice the motif of adding one to the interest rate, and then raising it to the number of payments. This becomes a problem when the periodic interest rate is very small and the number of payments very high, as we have in the above problem (10%/31’536’000 and 31’536’000 respectively).
The addition of 1 to a very small number is not easily represented by a floating point representation, rapidly losing information. There are ways around this but these can be absent on the earliest and inferior financial calculators. The worlds first financial calculator, the HP-80, was a milestone in computing, but even so, deposited money receiving a very small interest rate, would lose value with time.
Testing our rogue HP-12c, it returned a result of 331666.9849, from a true result of 331667.00669… giving it an accuracy2 of 7.2, somewhere between the HP-70 of 1974 (1.2!) and the HP-22 of 1975 (9), but far off the 10.6 achieved by the regular HP-12c and 12.2 of the HP-12c Precision.
When There is Little Interest
You wish to borrow $100’000, and repay over 480 payments at an interest rate of 0%. What are the monthly payments? If you then provide the calculated monthly payments, can the solver find the interest rate of zero again?
This puzzle was devised to test for the awkwardness of finding an interest rate of zero. But our rogue HP-12c unfortunately failed on the very first part of this problem returning an error. This part was easy and doesn’t need a financial calculator - simply take 100’000 and divide it by 480. Payments are -208.33 recurring.
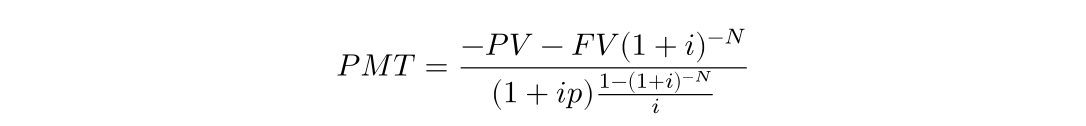
It is possible to re-arrange the TVM formula to algebraically calculate each unknown, except for one. Above is the formula fairly simplistically rearranged to solve for PMT. The equation looks complicated, but you can see the divide by ‘i’ in the bottom right. Now we might guess how the rogue HP-12c ran into trouble, as it likely attempted a divide by zero, a rookie mistake in the world of TVM solving.
Solving for ‘i’ is the special case, which requires an iterative approach, guessing and refining until you home in on the answer. There is a lot written on the pros and cons of various methods and the equations it is performed on, which would be easily another blog post. In this case, I gave the calculated PMT back into the solver manually, to see if it could solve the interest rate in this puzzle. Unfortunately the rogue HP-12 failed again, this time probably due to instability of the solver as ‘i’ approaches zero.
When There is Too Much Interest
Our poor HP-12c has collected a few black marks now, but there is hope.
What interest rate would balance a payment of $50 upfront, returning you $30 each year for 10 years, with $400 to be paid at the end?3
This would be a very unusual arrangement, and fittingly, there is an unusual answer in that there are two possible interest rates which would satisfy this. One is around 14.4% and the other 53.2%. No HP financial calculator (or many others) will attempt to return a result on this, but interestingly in a rare win, the rogue HP-12c gives us 14.44… and an accuracy of 8.7. Not bad.
So How Did This Happen?
The only conclusion is that someone, somewhere had a stab at completely re-writing the TVM solver. But this may be all we come to know of how this calculator came about. There are little clues on the device. The firmware is given as ChE–3198h and dated recently as 2023-03-19. The last known (and fully regular) firmware of the HP-12c was dated 2015-01-08.
The strange thing is that the HP-12c ROM is fairly easy to obtain, whether you are HP or not, so why re-write it? Did anyone in HP authorise a TVM solver returning different results. Was the device tested, and if so, would the tests have picked this up?
It looks like HP are already working hard to reverse this blot in the otherwise esteemed history of the HP-12c. A more recently ordered device from the Amazon Brazil store, bought just a few weeks before writing this, returned correct results and was using the 2015 firmware. Time will tell whether this rogue HP-12c will do any damage to its reputation, either in Brazil or in other parts of the world, and this will partly depend on how many are out in the wild, and whether HP are able to satisfactorily tidy this up.
These days pocket calculators are not generally used to give you a quote on your mortgage renewal. Instead, banks likely run their calculations on bespoke software or maybe a spreadsheet, though I’d be curious to know how optimised these are. Most numerical computer software represents numbers using a 64-bit binary representation (for which a penny is not precisely representable), and it would be interesting to see how this compares to the algorithms working on these decimal-coded calculator representations.
As it stands, the story of the rogue HP-12c may never be fully explained. For me it sums up a curiosity I’ve had in a mathematical formula, re-visiting some school maths and learning much I didn’t learn in school. I developed a huge respect for the engineering challenge faced over the years to improve the accuracy of TVM solving, as well as the ingenuity of such an optimised solving user-interface. The forensic tests tell us more about how these devices work beneath the surface, and while this article is on a very specific HP-12c calculator, each calculator has its own story to tell.
Acknowledgements
Thank you so much to my Brazilian friend who tirelessly worked with me across the Atlantic to test the rogue HP-12c and who eventually, in a cross-continental trust exercise, allowed me to order them another calculator, while relinquishing their own so I could get my hands on the real thing. Many thanks to everyone on the HP museums forum and the Swissmicros forum who have contributed to hundreds of threads on the HP-12c, as well as TVM solving in general. As a collective they have tested a huge number of devices with my collection of TVM puzzles, and were involved with working out whether this rogue variant existed or not. I also thank Swissmicros for the terrific DM42 calculator4, Thomas Okken for free42 (which runs on the DM42) and plus425, and Albert Chan who has worked on the TVM algorithms in Plus42 and provided much public and private advice on how it is best done. And of course, HP for having made, and continuing to make these great calculators in the first place.
-
https://www.alphr.com/technology/1001717/the-rebirth-of-the-hp-12c-how-one-man-reimagined-a-calculator-from-1981/ ↩
-
Defined here as the negative logarithm to base 10 of the absolute error. You can think of this as ballpark similar to the idea of digit-precision or ‘unit in the last place / ULP’ which is a simplistic way of measuring accuracy. ↩
-
https://www.hpmuseum.org/cgi-sys/cgiwrap/hpmuseum/archv021.cgi?read=234439 ↩
-
https://www.swissmicros.com/product/dm42 ↩
-
https://thomasokken.com/plus42/ ↩

